Los autómatas vienen a ser mecanismos formales que "realizan" derivaciones en gramáticas formales mediante la noción de reconocimiento, que dada una entrada produce una salida, es decir, calcula alguna función. Generalmente la entrada es una cadena de símbolos de un alfabeto, y la salida también, posiblemente sobre otro alfabeto.
Autómatas finitos:
Un autómata finito (FA) consiste en un conjunto finito de estados y un conjunto de transiciones de estado a estado, que se dan sobre símbolos de entrada tomados de un alfabeto ∑. para cada símbolo existe exactamente una transición a partir de cada estado (posiblemente al mismo estado).
A un FA se le asocia un grafo dirigido, conocido como diagrama de transiciones, de la manera siguiente:
Para encontrar mas informacion de autómatas de pila visitar: http://www.uhu.es/francisco.moreno/talf/docs/tema7.pdf
Autómatas lineales:
son autómatas de pila deterministas que a lo largo de su computación sólo hacen un ``cambio de turno''. A grandes rasgos, esto significa que toda computación consiste de un procedimiento de empilar consecutivamente para después pasar a des-empilar.
Ejemplo: Consideremos el lenguaje de palíndromos con una marca central:
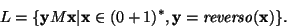
Consideremos el autómata de pila cuyas componentes son las siguientes:
y cuya función de transición actúa como sigue,
donde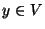 
y b es el símbolo ``blanco''. En cualquier otra instancia de t, ésta transitará al estado de fracaso. Es claro que este autómata de pila reconoce al lenguaje L.
Equivalencias de autómatas:
Dado un modelo de especificación de lenguaje, por ejemplo, el de los autómatas finitos, un problema decisional típico es el de determinar la equivalencia de dos representantes cualesquiera de ese modelo. los algoritmos generales de determinación y minimización de autómatas finitos, conjuntamente con la propiedad de unicidad del autómata mínimo, periten establecer un marco claro de comparación de autómatas y resolver el problema de la equivalencia de NFAs.
Por lo tanto:
Dados dos NFAs cualesquiera, M1 y M2, son equivalentes (reconocen el mismo lenguaje) si y sólo si los autómatas mínimos correspondientes de M1 y M2 son el mismo autómata.
Autómatas finitos:
Un autómata finito (FA) consiste en un conjunto finito de estados y un conjunto de transiciones de estado a estado, que se dan sobre símbolos de entrada tomados de un alfabeto ∑. para cada símbolo existe exactamente una transición a partir de cada estado (posiblemente al mismo estado).
A un FA se le asocia un grafo dirigido, conocido como diagrama de transiciones, de la manera siguiente:
 |
En la figura se ilustra un diagrama de transiciones, donde podemos saber que q0 es el inicio, por la etiqueta, y es el único estado final (en este caso) indicado por el doble círculo. El FA que se muestra solo acepta cadenas de ceros y unos, en las que el número de 0s y el número de 1s son pares.
Esto se entiende mejor si se considera que hay un control; el control empieza en q0 y termina en q0, cada entrada 0 requiere que el control cruce la línea horizontal a-b, mientras que una entrada 1 no. por lo que el control esta indicado por las rectas a-b y c-d.
Autómatas de pila:
Los Autómatas de Pila son una extensión de los AFD a los que se les añade una memoria (pila).
En la pila se almacenan símbolos de la cadena de entrada y de la gramática, así como caracteres especiales (#) para indicar el estado de pila vacía.
Las transiciones son de la forma: (p,x,s;q,t)
p=estado inicial
q=estado al que llega
x= símbolo de la cadena de entrada
s=símbolo que se des-apila
t=símbolo que se apila
(MORENO)
Para encontrar mas informacion de autómatas de pila visitar: http://www.uhu.es/francisco.moreno/talf/docs/tema7.pdf
Autómatas lineales:
son autómatas de pila deterministas que a lo largo de su computación sólo hacen un ``cambio de turno''. A grandes rasgos, esto significa que toda computación consiste de un procedimiento de empilar consecutivamente para después pasar a des-empilar.
Ejemplo: Consideremos el lenguaje de palíndromos con una marca central:
y b es el símbolo ``blanco''. En cualquier otra instancia de t, ésta transitará al estado de fracaso. Es claro que este autómata de pila reconoce al lenguaje L. Equivalencias de autómatas:
Dado un modelo de especificación de lenguaje, por ejemplo, el de los autómatas finitos, un problema decisional típico es el de determinar la equivalencia de dos representantes cualesquiera de ese modelo. los algoritmos generales de determinación y minimización de autómatas finitos, conjuntamente con la propiedad de unicidad del autómata mínimo, periten establecer un marco claro de comparación de autómatas y resolver el problema de la equivalencia de NFAs.
Por lo tanto:
No hay comentarios:
Publicar un comentario